A Nonlinear Dynamics nemzetközileg elismert szakfolyóiratban jelent meg Szederkényi Gábornak, a Pázmány Péter Katolikus Egyetem Információs Technológiai és Bionikai Kara egyetemi tanárának és társszerzőinek a Járványügyi beavatkozások tervezésének támogatása modell-prediktív szabályozással című tanulmánya. Már a cím elárulja, hogy mérnöki megközelítéssel napjaink súlyos problémáját állítják középpontba.
A kutatások megindítását és azok eredményének összegzését a mostani járvány hatására kezdték el?
Úgy gondoltuk, a magunk tudományos eljárásával reagálnunk kell járványtól terhes valóságunkra. Az általunk alkalmazott tudományos módszereket már korábban használtuk a kollégákkal és a hallgatókkal, elsősorban a mobil robotikai feladatok megoldásához. A pandémia kitörése után felvetődött az ötlet: ezeket a módszereket érdemes lenne járványmodelleken is tesztelni annak érdekében, hogy lássuk, mennyiben tudunk hozzájárulni a járvány kapcsán megfogalmazódó döntéstámogatási és irányítási problémák megoldásához.
Röst Gergely professzor vezeti a Járványmatematikai Modellező és Epidemiológiai Elemző Munkacsoportot. Hogyan jött létre az együttműködés a szegedi kutatókkal?
A járvány első szakaszában kormányzati szinten felmérték, mely felsőoktatási intézmények és hogyan tudnak hozzájárulni, akár elméleti, akár kísérleti módszerekkel a járvány elleni küzdelemhez. Ennek során vettük fel a kapcsolatot a Röst professzor által vezetett munkacsoporttal. Egyetemünk Információs Technológiai és Bionikai Karán széleskörű kutatómunka folyik bionikai módszerekkel a járványok terjedésének leírására és előrejelzésére. A rendszerelméleti megközelítés mellett a munka fontos része egy ágens alapú szimulátor fejlesztése, amely az egyes helyszínek, illetve akár az egyének szintjén is információt ad a járvány lefolyásáról.
 Ez azt jelenti, hogy matematikai modellek segítségével egyfajta „jóslásra” nyílik lehetőség?
Ez azt jelenti, hogy matematikai modellek segítségével egyfajta „jóslásra” nyílik lehetőség?
Az Interneten folyamatosan követhető a járvánnyal kapcsolatos adatok alakulása. Ismert a napi fertőzésszám, a kórházban ápoltak és az elhunytak száma. Mi, mérnökök jeleknek hívjuk ezeket az időben változó mennyiségeket. A jelek közötti összefüggések matematikai modellek segítségével adhatók meg. Ezek a modellek egyrészt a megértést, a folyamatok mélyebb feltárását, másrészt a közeljövő prognosztizálását is segítik.
Mire kerestek választ, és milyen eredményre jutottak?
Központi kérdésünket a következőképpen fogalmaztuk meg: hogyan lehet egyszerre védeni az emberéleteket, ugyanakkor fenntartani a kórházak működőképességét, miközben figyelembe kell venni azt is, hogy milyen korlátozások és mely időpillanatban szükségesek a súlyos gazdasági károk elkerüléséhez.
Az ellentmondó célok között egyensúlyt szükséges találni. Ebben segítenek azok a modellek, amelyek viszonylag pontosan meg tudják mondani, hogy ha végrehajtanak valamilyen intézkedést, az milyen irányban fogja befolyásolni a járvány menetét.
A kutatások mostani szakaszában meg lehet-e fogalmazni, hogy milyen konkrét információkkal, tanácsokkal tudtak szolgálni a döntéshozók számára?
További kutatások szükségesek ahhoz, hogy az eredményeket konkrét intézkedésekre lefordíthassuk. Arra vonatkozóan például, hogy a járvány elleni küzdelemben milyen intézményeket és mikor érdemes bezárni. Ebben az ügyben egyébként átfogó kari kutatás is folyik az említett ágens alapú szimuláció felhasználásával, összefüggésben a mi módszerünkkel. Mi egy szigorúsági indexet állítottunk fel az idő függvényében: mikor kell mindenképpen és milyen szigorúsággal beavatkozni ahhoz, hogy az említett hármas célt el lehessen érni.
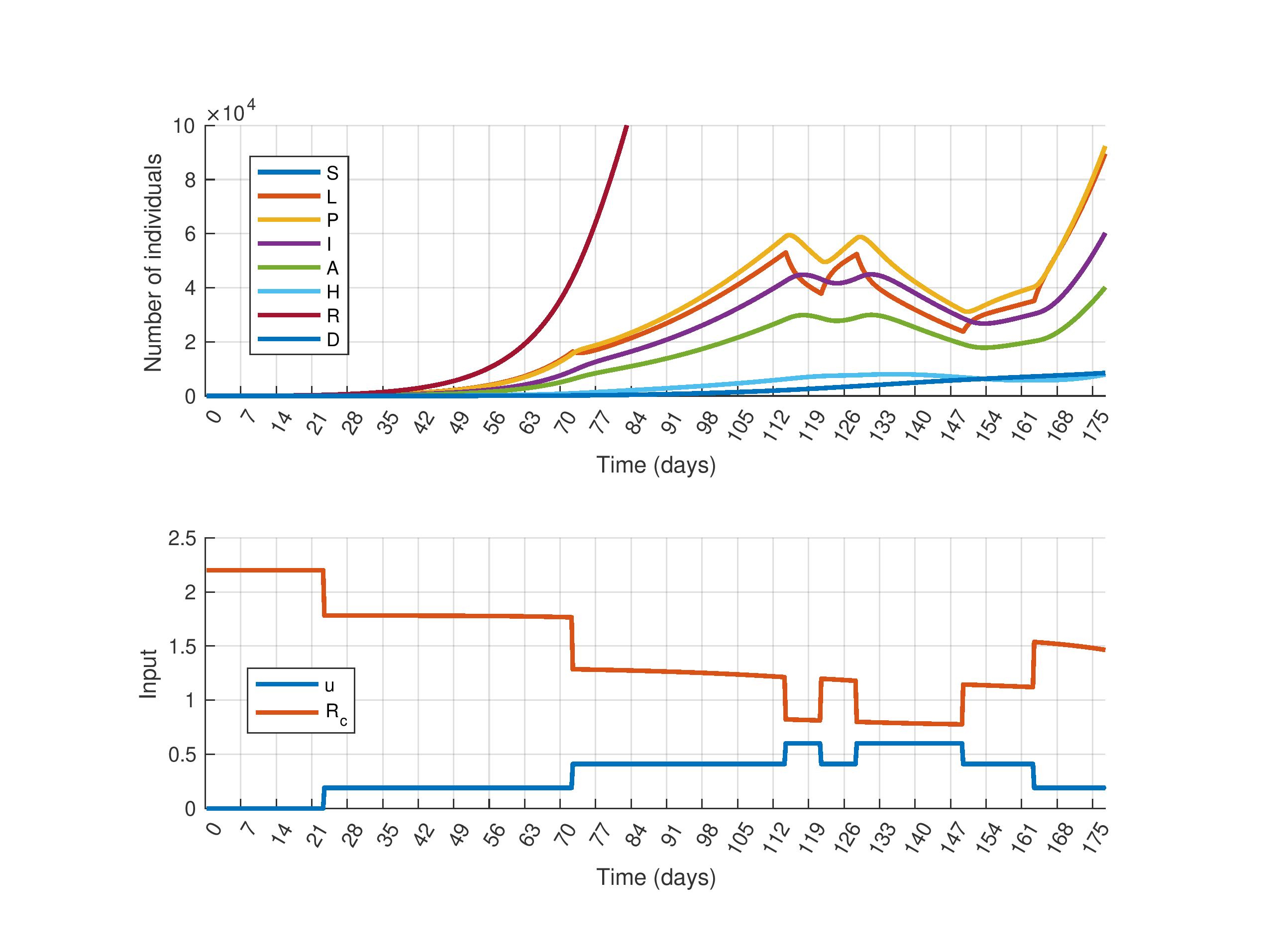
A konkrét modellen világosan, kvantitatív módon látható, hogy nem szabad túl sokat késlekedni egyes intézkedések bevezetésével, mert késedelem esetén ugyanazzal a költségráfordítással és munkával jóval kevesebb életet lehet megmenteni. Ki tudtuk számolni annak a kritikus időszaknak a határait, amelyeken belül mindenképpen be kell avatkozni.
Több forgatókönyvet is vizsgáltunk. Tavasszal a járvány teljes visszaszorítását tűzték ki célul, ennek érdekében igen szigorú intézkedések váltak szükségessé. Az őszi, második hullámban pedig mindenképpen el kell kerülni a kórházak túlterhelését. Ezek a célok különböző irányítási feladatok megfogalmazását igénylik.
Amikor bejelentenek bizonyos korlátozó intézkedéseket, akkor részben a munkájuk eredményét hallják vissza?
Mi jórészt absztrakt vizsgálatokat és modellezést végeztünk, illetve végzünk folyamatosan. Nem állíthatom, hogy eredményeinket közvetlenül felhasználják a döntéshozók, de ezek egybecsengenek a tavasszal, majd pedig ősszel meghozott intézkedésekkel. Ezeknek az intézkedéseknek a hatását megbízható számításokkal vissza tudjuk igazolni.
Számítási előrejelzések alapján mi mondható el a járvány lefutásáról a közeli jövőben?
Ahogyan nő az előrejelzés időtávja, annak arányában egyre bizonytalanabb prognózis adható. Annyit elmondhatunk, hogy a kórházban ápoltak számának csökkenése – amiben reménykedünk – már egy-két hete előrelátható. Prógnózisaink helytállónak bizonyultak, s ha a jelenlegi korlátozó intézkedéseket még mintegy két hónapig fenntartják, akkor várhatóan lényegesen kevesebb beteget kell majd kórházban ápolni. Ötvennapos távlatban számuk kevesebb, mint a felére csökkenhet.
A jelek, a mennyiségek alapján folyamatosan frissítik az eredményeket?
Igyekszem naponta frissíteni a modell alapú prognózist, és ellenőrizzük, hogy megfelelő-e az adott pillanatban használt modell. A paramétereket ugyanis időnként pontosítani kell.
Az eredmények a publikációkban jelennek meg, vagy közvetlenül is továbbítják azokat?
Remélem, hogy újabb publikációk is születnek kutatásainkból. Folyamatos kapcsolatban állunk a Röst Gergely professzor által vezetett Járványmatematikai Modellező és Epidemiológiai Elemző Munkacsoporttal. Ők más szempontból, más eszközökkel végeznek hasonló számításokat, s ezek mostanáig megerősítették egymást.
Mindezek után hogyan foglalná össze tanulmányuk újdonságát?
Sokan kutatnak hasonló problémákat, ezért maga a rendszerelméleti megközelítés nem mondható egyedinek. Mi sokféle korlátozó feltételt, illetve előírást kezelünk számítási keretrendszerünkben, s ezek között esetleg még preferált logikai kapcsolatok is megadhatók. Ebben a pillanatban ez adja meg tanulmányunk különlegességét, ilyen módszertannal ugyanis eddig még nem jelent meg hasonló témájú tanulmány.
Kik vesznek részt a tanulmányhoz kapcsolódó kutatócsoportban?
A szabályozás koncepcionális tervezését Péni Tamással, a Számítástechnikai és Automatizálási Kutatóintézet tudományos főmunkatársával közösen végeztük el. A PPKE-ITK-s kutatócsoportom tagja Csutak Balázs mesterszakos hallgató, aki hasznos és sokszor kritikus számításokat végzett el, miközben nagyon sokat tanult is.
Készítette: PPKE Kommunikáció/E.I.
Fotó: PPKE, Szederkényi Gábor



